Our paper entitled “A General Iterative Extended Kalman Filter Framework for State Estimation on Matrix Lie Groups” is accepted by CDC 2023.

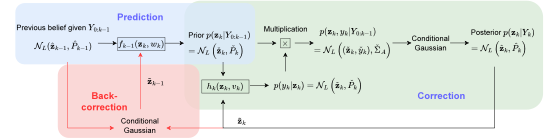
In this paper, we focus on state estimation problem for nonlinear systems on joint matrix Lie group and Euclidean space. We propose a general iterative Kalman filter, aiming to integrate the prediction step into the iteration scheme, which is not considered in the conventional iterative extended Kalman filter framework. Such an extra iteration scheme in the prediction step helps improving the accuracy of probability density function propagation through nonlinearities, which can further lead to more accurate estimations of the system states. In addition, the proposed framework unifies the Kalman filter based estimation schemes on studied manifold by adopting the perspective from Gaussian Bayesian inference. The improvement of the proposed framework is illustrated by the ES-GIKF algorithm that is instantiated from the proposed framework in a numerical simulation.