Our paper entitled “A Geometric Sufficient Condition for Contact Wrench Feasibility” is accepted by RA-L 2022 and will be presented at IROS 2023.

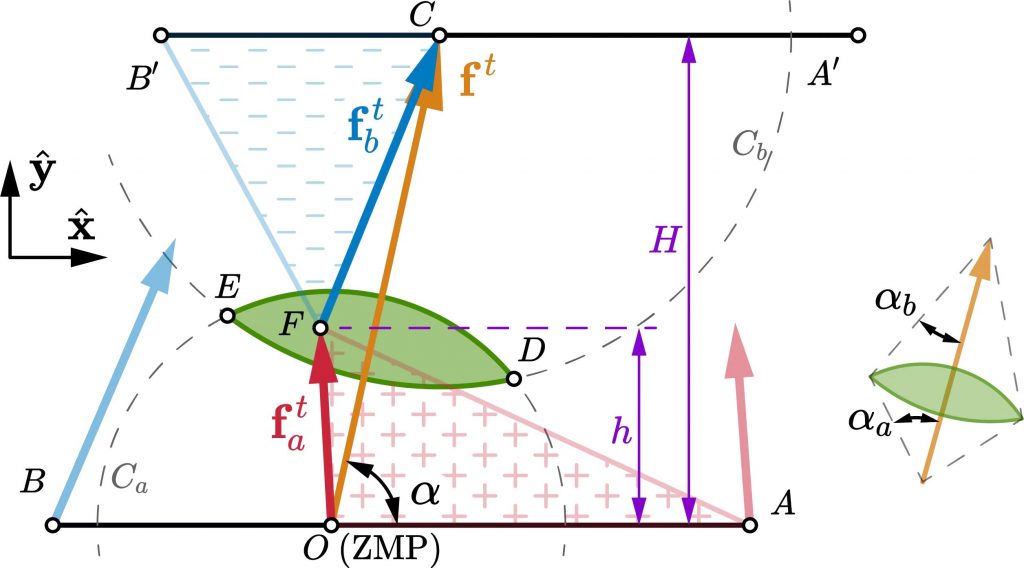
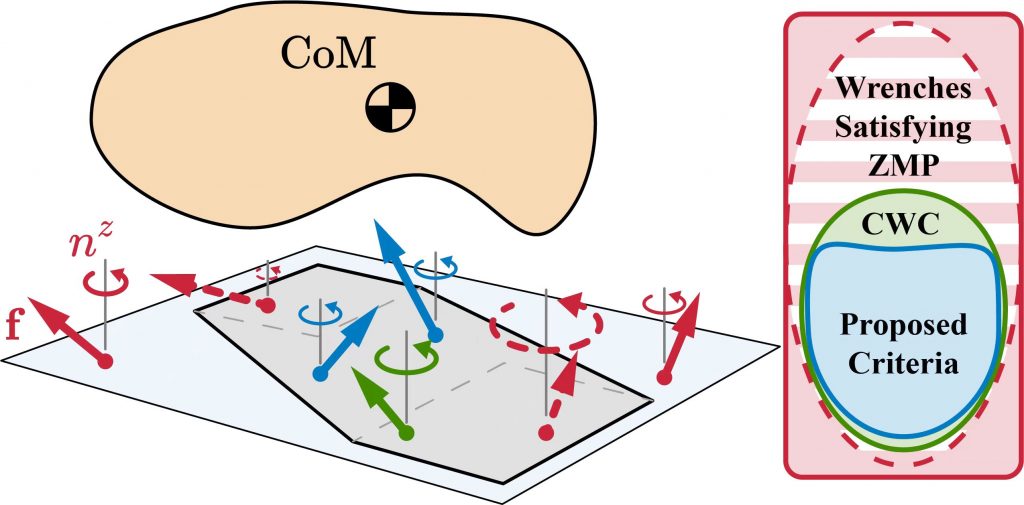
A fundamental problem in legged locomotion is to verify whether a desired trajectory satisfies all physical constraints, especially those for maintaining contacts. Although foot tipping can be avoided via the Zero Moment Point (ZMP) condition, preventing foot sliding and twisting leads to the more complex Contact Wrench Cone (CWC) constraints. This paper proposes an efficient algorithm to certify the inclusion of a net contact wrench in the CWC on flat ground with uniform friction. In addition to checking the ZMP criterion, the proposed method also verifies whether the linear force and the yaw moment are feasible. The key step in the algorithm is a novel exact geometric characterization of the yaw moment limits in the case when the support polygon is approximated by a single supporting line. We propose two approaches to select this approximating line, providing an accurate inner approximation of the ground truth yaw moment limits with only 18.80% (resp. 7.13%) error. The methods require only 1/150 (resp. 1/139) computation time compared to the exact CWC based on conic programming. As a benchmark, approximating the CWC using square friction pyramids requires similar computation time as the exact CWC, but has > 19.35% error. Unlike the ZMP condition, our method provides a sufficient condition for contact wrench feasibility.