Our paper entitled “An Augmented Lagrangian Perspective on Differential Flatness-Based Control of Dual Spring-Loaded Inverted Pendulum Model” accepted by LCSS 2024.

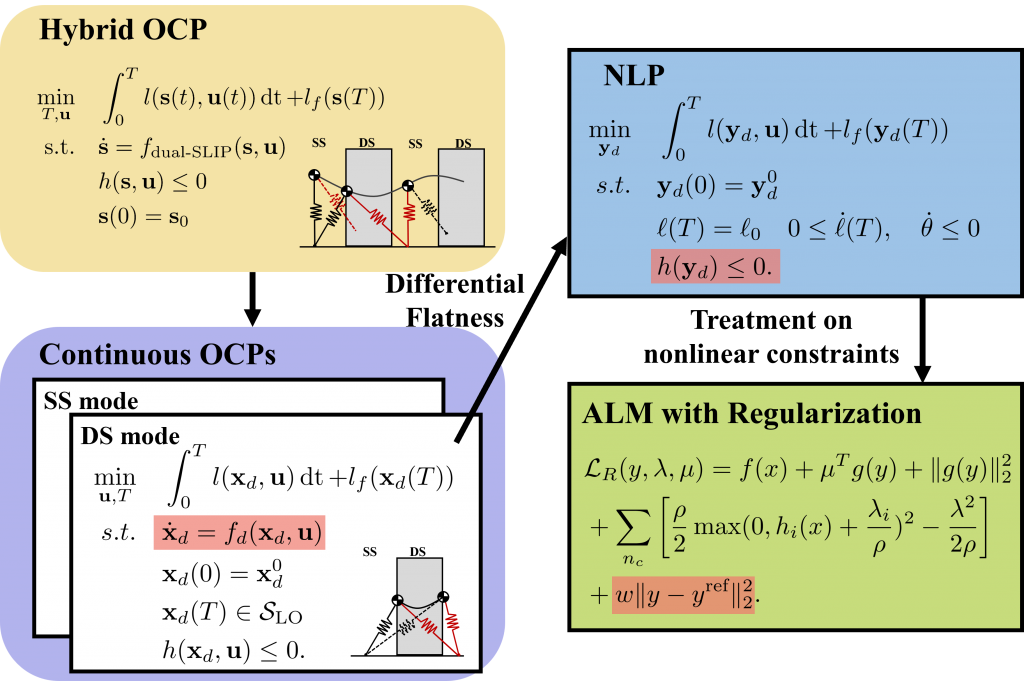
Controller synthesis for bipedal legged locomotion is challenging. The spring-loaded inverted pendulum (SLIP) model is an effective simplified model for planning bipedal locomotion. In this letter, we focus on the optimal control problem (OCP) of an actuated dual SLIP model, which enables active control for articulated bipeds. For such a complicated nonlinear optimal control problem,differential flatness-based approaches have been shown to be valid. Such approaches leverage the differential flatness property of the underlying dynamics to transform the original nonlinear hybrid OCP into a number of polynomial optimizations. Despite the effectiveness, neither theoretical justification nor convergence analysis have been provided to support the rigorousness of such methods. In this letter, we aim to bridge this gap by analyzing the class of differential-flatness-based approaches from a Lagrangian-based perspective. To this end, we show that the differential-flatness-based methods can be viewed as a modified Augmented Lagrangian Method (ALM) with a regularization term about a feasible passive trajectory from the passive Dual SLIP model. In this letter, we show that our method converges to the optimal solution and improves both the convergence rate and solution quality compared to standard ALM. In numerical experiments, the performance of the proposed algorithm exhibits faster convergence and lower feasibility errors compared to existing methods. In addition, our algorithm achieves consistent performance across various initializations and can offer an excellent initialization for standard ALM.