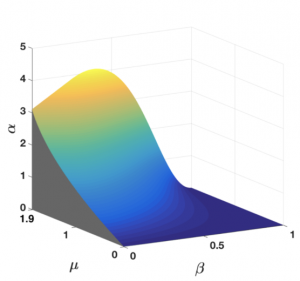
Our new paper entitled “Analytical convergence regions of accelerated gradient descent in nonconvex optimization under Regularity Condition” is accepted by Automatica. This paper studies a class of nonconvex optimization problems whose cost functions satisfy the so-called Regularity Condition (RC). Empirical studies show that accelerated gradient descent (AGD) algorithms (e.g. Nesterov’s acceleration and Heavy-ball) with proper initializations often work well in practice. However, the convergence of such AGD algorithms is largely unknown in the literature. The main contribution of this paper is the analytical characterization of the convergence regions of AGD under RC via robust control tools. Since such optimization problems arise frequently in many applications such as phase retrieval, training of neural networks and matrix sensing, our result shows promise of robust control theory in these areas.